Linear algebra for machine learning
- Distance between two points
- Dot product and angle between 2 vectors
- Equation of a line, plane
- Projection of a vector
- Distance of a point from a plane
- Equation of a circle
1. Distance between two points
-
Let A & B be two points in 2 dimensional geometry.
\[A = (x_1, y_1)\] \[B = (x_2, y_2)\]-
Euclidean distance
\[distance(A,B) = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}\]Example:
\[A = (2, 2)\] \[B = (4, 4)\]
\[distance(A,B) = \sqrt{(2-4)^2 + (2-4)^2} = \sqrt{8} =2\sqrt{2}\]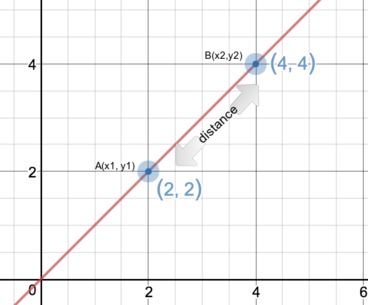
-
Manhatten distance
\[distance(A,B) = |x_1-x_2| + |y_1-y_2|\]In case the movement on diagonal side is allowed,
\[distance(A,B) = max(|x_1-x_2| , |y_1-y_2|)\] -
Minkowski distance (Generalisation)
where p = 1, 2, 3 ... if p == 1, minkowski distance will converge into Manhatten distance if p == 2, minkowski distance will converge into Euclidean distance -
-
If A & B points are in n dimensional geometry, then
\[A = ( {x_{a1},x_{a2}, x_{a3}, ....x_{an}} )\] \[B = ( {x_{b1},x_{b2}, x_{b3}, ....x_{bn}} )\]Then,
-
Euclidean distance(A,B) = \(\sqrt{(x_{a1}-x_{b1})^2 + (x_{a2}-a_{b2})^2+ ... + (x_{an}-x_{bn})^2}\)
-
Manhatten distance(A,B) = \(|x_{a1}-x_{b1}| + |x_{a2}-a_{b2}| + .... + |x_{an}-a_{bn}|\)
-
Minkowski distance(A,B) = \(({|x_{a1}-x_{b1}|^p + |x_{a2}-a_{b2}|^p+ ... + |x_{an}-x_{bn}|^p})^{1/p}\)
-
2. Dot product and angle between 2 vectors
a & b points are in n dimensional vectors, i.e.,
\[a = ({a_1,a_2,a_3, ... a_n})\] \[b = ({b_1,b_2,b_3, ... b_n})\]Dot product of a & b = a.b
\[a.b = a_1b_1 + a_2b_2 + a_3b_3 + ... + a_nb_n\]It is same as matrix multiplication of a & b vectors, i.e.,
\[a.b = \begin{bmatrix}{a_1} & {a_2} & {a_3} & {a_4} ..... {a_n}\end{bmatrix} * \begin{bmatrix}{b_1}\\{b_2} \\ {b_3} \\ {b_4} \\ . \\ . \\ {b_n}\end{bmatrix}\]Note: By default, a vector is column vector if not mentioned explicitly. So here a & b are column vectors
\[a.b = a^Tb\]Also we know that : \(a.b = |a| * |b| * Cos(\theta)\) (proof)
where a = distance of a from origin & b = distance of b from origin
\[\theta =arccos(\frac{a^T.b}{|a| * |b|})\]3. Equation of a line, plane
Line in 2D = Plane in 3D = hyper plane in nD
-
2 dimensional geometry
The equation of a line in 2D is \(ax+by+c=0\)
which can also be written as \(w_1x_1+w_2x_2+c=0\)
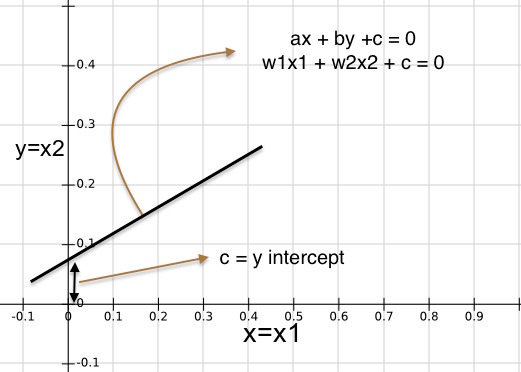
If line passes through origin (0, 0) then y-intercept becomes 0. So equation becomes
\[w_1x_1+w_2x_2=0\] -
3 dimensional geometry
Equation of a plane in 3D passing through the origin (0,0)
\[w_1x_1+w_2x_2+w_3x_3=0\] -
n dimensional geometry
Equation of a plane in nD passing through the origin (0,0)
\[w_1x_1+w_2x_2+w_3x_3+...+w_nx_n=0\]i.e.,
\[\sum_{i=1}^n w_ix_i = 0\] \[w^Tx = 0\] \[w.x=0\]We know that if a.b = 0, then a is perpendicular to b ( \(\because\) if \(Cos(\theta)\) = 0, then \(\theta = 90^\circ\))
\(\therefore\) \(w\) is perpendicular to any point on plane \(x\), provided plane passes through origin
4. Projection of a vector
Let \(a\) & \(b\) be two vectors and \(\theta\) be the angle between them.
\(d\) is the projection of \(a\) on \(b\)
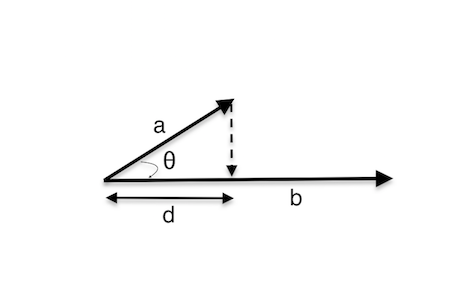
Then
\[Cos(\theta) = \frac{|d|}{|a|}\] \[|d|= |a|.Cos(\theta)\]Multiply both sides by \(|b|\)
\[|b|.|d|= |a|.|b|.Cos(\theta)\]We know that \(a.b = |a| * |b| * Cos(\theta)\)
\[\therefore d = \frac{a.b}{|b|}\]If \(b\) is a unit vector, then \(d = a.b\)
5. Distance of a point from a plane
Let \(p\) be any point in \(n\) dimensional geometry, which is at a distance \(d\) from the hyper plane \(\pi_n\).
Let \(w\) be a vector passing through origin (0,0)
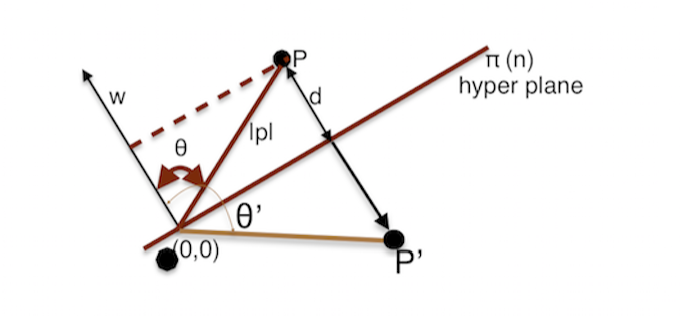
Distance of point \(p\) from the plane \(\pi\) is the projection of \(p\) on \(w\)
\(\therefore\) projection of \(p\) on \(w\) = \(d\)
\[d = \frac{w.p}{|w|}\]If \(w\) is a unit vector, then \(d = w.p\)
\(d\) is positive since \(\theta\) is less than 90\(^\circ\)
Similary we can calculate the distance of the point \(p'\) from the plane \(\pi_n\). Since \(\theta'\) is greater than \(90^\circ\), the distance will be negative.
In this way, we can decide in which side of the plane a point lies.
6. Equation of a circle
Let \(C\) be the center of the circle & \(P\) be the locus of the center of the circle.
\[C = (x`, y`)\] \[P = (x, y)\]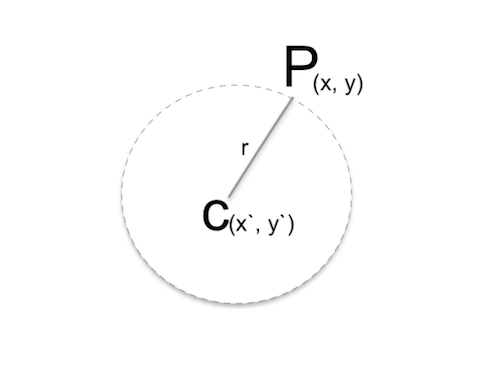
Let \(r\) be the radius of the circle
\[r = \sqrt{(x-x`)^2 + (y-y`)^2}\] \[=> (x-x`)^2 + (y-y`)^2 = r^2\]If the center of the cirlce is origin i.e., \((0, 0)\), then the equation of the circle is given as
\[\boldsymbol{ x^2 + y^2 = r^2}\]I will update this post as & when I get time. Please contact me regarding any queries or suggestions.